Cours : Nombres entiers et décimaux 2024

Cours de mathématiques 6éme : Nombres entiers et décimaux
Dans cet article nous allons développer point par point le cours de 6éme sur les nombres entiers et décimaux, dans un premier temps nous allons définir le contenu du cours, les compétences exigibles ainsi que l’objectif final de notre cours de mathématiques.
Enfin à la fin de cet article vous trouverez le lien vers une série d’exercices corrigés spécialement conçue pour vous afin de tester vos connaissances.
| Contenus | Compétences exigibles | Commentaires |
|---|---|---|
| Nombres entiers et décimaux : écriture et opérations. Ranger des nombres donnés en écriture décimale . | Utiliser l’écriture décimale et en connaître le sens . Sur une droite graduée : – Lire l’abscisse d’un point ou en donner l’encadrement, – situer un point d’abscisse donnée . | On consolidera et on enrichira les acquis de l’école élémentaire relatifs à la numération et au sens des opérations en les mobilisant dans l’étude de situations rencontrées au collège . On tendra ainsi à ce que la maîtrise des techniques opératoires devienne suffisante pour ne pas faire obstacle à la résolution de problèmes . |
Nombres entiers
1, 2, 3, 4, 5, 6, 7, 8, 9 et 0 sont les 10 chiffres qui permettent d’écrire tous les nombres, de même que les lettres de A à Z permettent d’écrire tous les mots.
Exemple :
1 054 est un nombre de 4 chiffres.
7 est un nombre d’un seul chiffre.
Pour pouvoir lire les grands nombres facilement, on regroupe les chiffres par tranches de 3 en partant de la droite.
Exemple :
1049658723 s’écrit 1 049 658 723 et se lit « un milliard, quarante neuf millions, six cent cinquante huit mille, sept cent vingt trois ».
| Tranche des milliards | Tranche des millions | Tranche des milliers | Tranche des unités | ||||||||
| C | D | U | C | D | U | C | D | U | Centaines | Dizaines | Unités |
| 1 | 0 | 4 | 9 | 6 | 5 | 8 | 7 | 2 | 3 | ||
Nombres décimaux
Exemple :
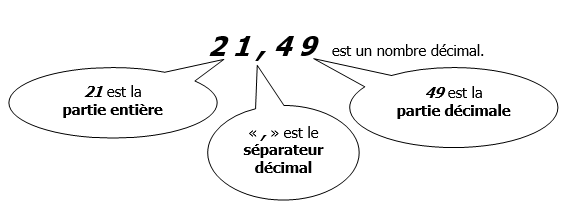
Ici, le 4 est le chiffre des dixièmes et le 9 est le chiffre des centièmes.
| Partie entière | Partie décimale | |||||
| Dixièmes | Centièmes | Millièmes | dix-milièmes | Cent-millièmes | Millionièmes | |
| 2 1 , | 4 | 9 | ||||
On dit qu’un nombre est « entier » lorsqu’il n’a pas de partie décimale (c’est à dire qu’elle est nulle) et donc pas besoin de virgule.
Ordre et comparaison de nombres
- « < » signifie « est inférieur à »
- « > » signifie « est supérieur à »
Exemple :
5 > 2 1,2 < 1,21 4 > 3 8,9 < 9,8
On dit que des nombres sont rangés par ordre croissant quand ils sont classés « du plus petit au plus grand ».
Exemple :
2,8 < 5,9 < 12,36
On dit que des nombres sont rangés par ordre décroissant quand ils sont classés « du plus grand au plus petit ».
Exemple :
1,96 > 1,192 > 1,0257
Axe gradué
Dans cette partie du cours nous allons voir les axes gradués, On repère un point sur un axe gradué grâce à un nombre qu’on appelle son abscisse.
Exemple :
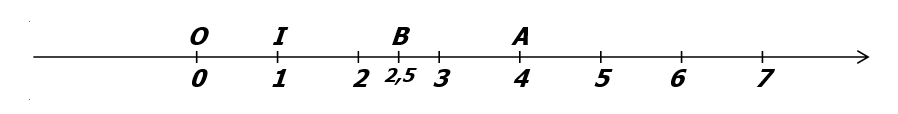
- O est l’origine de cet axe gradué.
- Le point A est repéré par le nombre 4 : On dit que 4 est l’abscisse de A.
- B est le point d’abscisse 2,5.
- La distance entre les points d’abscisse 0 et 1 est l’unité de longueur.
Enfin, gardez en tête qu’en utilisant pour abscisses des nombres décimaux, on ne peut pas repérer les points qui se trouvent à gauche de O.
Nous espérons enfin que vous avez réussi à comprendre l’essentiel de ce cours de mathématique de 6éme sur les nombres entiers et décimaux. Sachez que si vous souhaitez vous entrainer pour le jour de l’examen vous pouvez utiliser notre recueil gratuit d’exercices corrigés que vous trouverez en cliquant sur le lien ci-dessous :



Un commentaire