Exercices corrigés suites numériques 2024

Exercices corrigés suites numériques

Définition de suites

Dans cette partie d’exercices corrigés suites numériques nous allons apprendre les définitions des suites numériques.

Pour chacune des suites (u_n) définies ci-dessous, calculer u₁, u₂, u₃ et u₆.

1. $$U_n=\;\frac{7n\;-\;2}{n\;+\;4}$$
2. La suite ci-dessous :

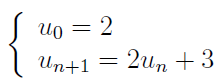
3. U_n est le n^ième nombre premier.
4. U_n est la somme des n premiers nombres pairs strictement positifs.
5. U_n est le nombre de diviseurs positifs de n.
6. J’ai mille euros 1000€ sur mon livret A au taux de 2,5% par an. U_n est la somme dont je dispose à la n^ième année.
7. U_n est la nième décimale du nombre π.

Sens de variation d’une suite

Dans cette partie d’exercices corrigés suites numériques nous allons apprendre à trouver le sens de variation d’une suite numérique.

Etudier le sens de variation d’une suite Un dans chacun des cas ci-dessous :

1. $$U_n\;=\;3n\;-\;5$$
2. $$U_n\;=\;-n^2+\;5n\;-\;2$$
3. $$U_n\;=\;\frac{n+1}{n+2}$$
4. $$U_n\;=\;\frac{3^n}2$$
5. $$U_n\;=\;\sqrt{n^2+3}$$
6. $$U_n\;=\;\left(-\frac12\right)^n$$
7. La suite ci-dessous:

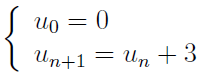
8. La suite définie ci-dessous :

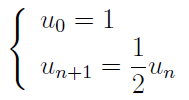
9. $$U_n\;=\;\sqrt{n+1}\;-\;\sqrt n$$

Majoration et minoration d’une suite

Dans cette partie d’exercices corrigés suites numériques nous allons apprendre comment montrer la majoration et la minoration des suites numériques.

1. Soit la suite (u_n) définie pour tout n ∈ N^⋆
   Par :
   $$U_n\;=\;5-\frac1n$$
   Montrer que la suite (u_n) est bornée.
2. Soit la suite (u_n) définie pour tout n ∈ N^⋆
   Par :
   $$U_n\;=\;\frac{2n+1}{n+2}$$
   
   (a) Montrer que la suite (u_n) est majorée par 2.
   (b) Montrer que la suite (u_n) est minorée par 0.5
3. Soit la suite (u_n) définie pour tout n ∈ N^⋆ par :
   $$U_n\;=\;-n^2+8n\;+\;1$$
   Montrer que (u_n) est majorée par 17.
4. Soit la suite (u_n) d´efinie pour tout n ∈ N^⋆ par :
   $$U_n\;=\;\sqrt{n+1}-\sqrt n$$
   Montrer que (u_n) est majorée et minorée.

Les suites arithmétiques

Dans cette série d’exercices corrigés suites numériques, toutes les questions sont indépendantes les unes des autres, nous allons pas à pas apprendre les suites arithmétiques.

1. On définit pour tout n la suite (u_n) par :
   $$U_n\;=\;3n-2$$
   Montrer que (u_n) est une suite arithmétique.
2. Soit (u_n) une suite arithmétique de premier terme U₀ = 5 et de raison
   $$\frac13$$
   
   Calculer le 9ième terme de cette suite, puis calculez la somme suivante :
   $$S\;=\;U_0\;+\;U_1\;+\;U_2\;….\;+\;U_8$$
3. Soit (V_n) une suite arithmétique de premier terme V₁ = 2 et de raison −2.
   Calculer U₁₅, puis la somme :
   $$sum_{}\;=\;V_7\;+\;V8\;+\;V_9\;….\;+\;V_{15}$$
4. Calculer :
   $$S\;=\;11\;+\;14\;+\;17\;+\;.\;.\;.\;+\;170\;+\;173$$.

Les suites géométriques

Dans cette série d’exercices corrigés suites numériques, toutes les questions sont indépendantes les unes des autres, nous allons pas à pas apprendre les suites géométriques.

1. Soit la suite (u_n) définie pour tout n ∈ N par :
   $$U_n\;=\;\frac{7^{n+1}}5$$
   Montrer que (u_n) est une suite géométrique et déterminer sa raison et son premier
   terme.
2. Soit (u_n) une suite géométrique de premier terme :
   $$U_1\;=\;\frac1{81}$$
   
   et de raison −3.
   Calculer u₇, puis :
   $$S\;=\;u_1\;+\;u_2\;+\;u_3\;….\;+\;u_7$$
3. Calculer :
   $$\sum_{}\;=\;1\;+\;2\;+\;4\;+\;8\;+\;.\;.\;.\;+\;4\;096.$$

Les Suites Arithmético-géométriques

Veuillez noter que cet exercice est très classique, en effet d’après nos statistiques et sur une année complète de terminale S vous avez de très fortes chances de voir ce type d’exercice, tout en sachant que les suites sont des exercices très classiques qui reviennent très souvent dans les sujets du baccalauréat.

Dans cette partie d’exercices corrigés suites numériques, nous allons voir pas à pas les suites arithmético-géométriques.

Considérons la suite (u_n) de nombres réels, définie pour tout entier n > 0 par la
relation de récurrence suivante :
$$U_{n+1}\;=\;\frac12\;u_n+3$$

et la relation initiale :
$$U_0\;=\;2$$

1. Calculer u₁, u₂ et u₃.
2. (Vn) est la suite définie pour tout entier naturel n par :
   $$V_n\;=\;u_n\;-\;6$$
   Démontrer que (v_n) est une suite géométrique et déterminer sa raison.
3. Pour tout entier naturel n, exprimer (v_n) puis (u_n) en fonction de n.
4. Calculer :
   $$S\;=\;v_0\;+\;v_1\;+\;v_2\;….\;+\;v_9$$
   Puis calculer :
   $$Z\;=\;u_0\;+\;u_1\;+\;u_2\;….\;+\;u_9$$

Représentation graphique d’une suite

Dans cette partie d’exercices corrigés suites numériques, nous allons voir pas à pas comment représenter graphiquement une suite numérique.

On considère les suites (u_n) et (v_n) définies pour tout entier naturel n par :

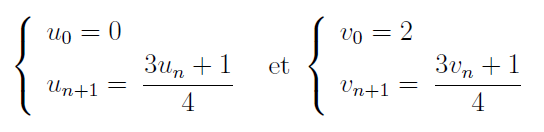
1. Calculer u₁, u₂, u₃ d’une part et v₁, v₂, v₃ d’autre part.
2. Dans un repère orthonormal (O;i, j) , d’unité graphique 5 cm, tracer les droites D et ∆ d’équations respectives:
   $$y\;=\;\frac{3x\;+1}4$$
   et
   $$y\;=\;x$$

Utiliser D et ∆ pour construire sur l’axe des abscisses les points A₁, A₂, A₃ d’abscisses respectives u₁, u₂, u₃ ainsi que les points B₁, B₂, B₃ d’abscisses respectives v₁, v₂, v₃.

3. On considère la suite (s_n) définie pour tout entier naturel n par :
   $$s_n\;=\;u_n\;+\;v_n$$

(a) Calculer s₀ , s₁, s₂ et s₃. À partir de ces résultats que peut-on conjecturer pour la suite (s_n) ?

(b) Admettons que la suite (s_n) est une suite constante égale à 2. (la démonstration n’est pas du programme de première Lycée).

4. On considére la suite (d_n) définie pour tout entier naturel n par :
   $$d_n\;=\;v_n\;+\;u_n$$
   
   (a) Montrer que la suite (d_n) est géométrique.
   (b) Donner l’expression de d_n en fonction de n.
5. En utilisant les questions 3.(b) et 4.(b), donner l’expression de u_n et de v_n en fonction de n.

6. Calculer la limite de chacune des suites (u_n) et (v_n).

Problème de Mathématiques

Dans cette dernière partie d’exercices corrigés suites numériques, nous allons traiter un problème réel de la vie courante dans lequel les connaissances des suites numériques vous permettront de faire le bon choix.

Une personne loue une maison a partir du premier janvier 1991. Elle a le choix entre deux formules de contrat. Dans les deux cas, le loyer annuel initial est de 4800€ et le locataire s’engage à occuper la maison pendant 9 années complètes. Les valeurs décimales seront arrondies, si nécessaire, au centime près.

1. Le premier contrat :
   Dans ce premier contrat le locataire accepte une augmentation annuelle de 5% du loyer de
   l’année précédente.
   (a) Calculer le loyer u₁ payé lors de la deuxième année.
   (b) Exprimer un (loyer payé lors de la (n + 1)ième année) en fonction de n.
   (c) Calculer u₈.
   (d) Calculer la somme payée à l’issue des 9 années de contrat.
   
2. Le deuxième contrat :
   Le locataire accepte une augmentation annuelle forfaitaire de 300€ du loyer de l’année précédente.
   (a) Calculer le loyer v_n payé lors de la deuxième année.
   (b) Exprimer v_n (loyer payé lors de la (n + 1)ième année) en fonction de n.
   (c) Calculer la somme payée à l’issue des 9 années de contrat.
   
   Question à 1 Million, d’après vos calculs quel est le contrat le plus avantageux ? 😉

Les suites numériques sont très utilisées dans différents secteurs comme les banques, les compagnies d’assurance, les marchés financiers etc…

Travaillez avec beaucoup de sérieux ces exercices corrigés suites numériques avant de regarder les solutions.